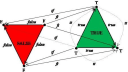
Qualities as Commutative Triangles: Quality is a functor q on a cohesive category C and valued in a quality type T. Cohesion of a category C is relative to a category S of sets with its four functors: pieces c!: C –> S, discrete c*: S –> C, points c*: C –> S & codiscrete c!: S –> C satisfying: components -| discrete -| points -| codiscrete (-| denotes left adjoint). Quality type T is also relative to S with its functors satisfying: pieces t! = points t*: T –> S & codiscrete t! = discrete t*: S –> T.
In this note, we will see how the scientific study of space developed, beginning with a naïve notion of container (with its attendant outside) to a theory abstracted from a conscious participation in the scientific practice of mathematical study of spaces from within, i.e. in terms of cohesion and qualities (form and substance).
What is SPACE? A space is an object in a category of spaces (Lawvere, 2010, 2015). This answer in turn raises questions such as: What is a category? Before we explore further along these lines, let us look at our naïve notion of space. Space is a container … “inhabited by the accidents of matter” (Cartier, 2001); it’s a stage for events, an arena of change, of quantitative variation, and of becoming (Lawvere, 1992). Simply put, space is like a blank slate used to draw figures of all sorts. This ancient idea of space is dialectical: container vs. contents, which continues to fuel the ongoing refinement of the concept of space. Containers (e.g., rooms) are made of locations or positions where contents (tables and chairs) can be placed. With positions objectified as points, and with the added realization that positions can be near or far apart, we arrive at an understanding of space as a collection or set of points with some additional structure. These sets equipped with structure are categories; and a category is a mathematical universe of discourse (Lawvere and Rosebrugh, 2003, pp. 239-240; Lawvere and Schanuel, 2009, pp. 135-151). The constituents of space i.e., points were initially thought of as having no structure, like the elements of a set. Subsequently, points were recognized as an objectification of constancy: a limit case of zero variation (Lawvere, 1975). Seen from this new perspective, points are not that different from figures, albeit special (or singular). It is possible, with points considered as figures of special shape: the shape of a category’s terminal object, to have spaces without their, what were hitherto considered the basic building blocks i.e., points (Lawvere and Schanuel, 2009, pp. 230-235). More importantly, the geometry of a space is determined by figures and their incidence relations within the space (Lawvere and Schanuel, 2009, pp. 370-371).
The container is, thus, determined by its contents, which is reminiscent of the content-addressable memories of neural networks (Hopfield, 1982). This paradigm shift—from space as a container existing in-and-of itself to space as a structure of the relations between its contents—mirrors a parallel development in physics (Roy, 1998, pp. 222-229).
The reach of the figural-turn of our mathematical understanding of space extends far beyond space—all the way to bridging the abyss between space and symbol. With symbolic logic as the algebra of [spatial] parts (Lawvere and Rosebrugh, 2003, pp. 193-212), we have rudiments of a scientific account of how the commonplace experience of thinking about space all around us works:
“Human activities such as building a house, navigating the solar system, require plans that can work. Planning any such undertaking requires the development of thinking about space. Each development involves many steps of thought and many related geometrical constructions on spaces. Because of the necessary multistep nature of thinking about space, uniquely mathematical measures must be taken to make it reliable. Only explicit principles of thinking (logic) and explicit principles of space (geometry) can guarantee reliability. Category theory permitted making the principles of logic and geometry explicit by discovering the common form of logic and geometry. The principles of both logic and geometry rest on ‘naturality’ of the transformations between spaces and the transformations within thought” (Picado, 2007).
A fascinating recent development in the mathematical study of space is the recollection of Maxwell’s profound insight: description of the nature of space depends on the needs of investigation (Lawvere, 2007). In studying the resultant categories of space (e.g., combinatorial, smooth), it became clear that COHESION is the defining attribute of space (Lawvere, 1994a; Lawvere and Rosebrugh, 2003, p. 232). Cohesive spaces, in contrast to discrete spaces such as sets, are characterized by a truth value object that allows true to become false (Grothendieck, 1983; Lawvere, 2003). Moreover, with quality as that which remains upon identifying all quantitative variations (Lawvere, 1992), qualities of cohesive spaces are defined (Lawvere, 2008). The essence or theory (adequate to complete characterize every space and to tell apart transformations of spaces) of any cohesive category of spaces is an intensive quality, while the form or logic (algebra of parts) of a cohesive category of spaces is an extensive quality. The axiomatization of cohesion can be used to formalize the unity or cohesiveness of conscious experiences (Roskies, 1999); while the definition of quality can be used to formalize the qualitative universals given in our conscious experiences i.e., qualia (Lewis, 1929, p. 121).
Within mathematical experience, the study of space gave rise to various concepts (e.g., topos; Lawvere, 2014; Lawvere and Rosebrugh, 2003, pp. 245-247), and the thus abstracted theories (e.g., dynamical evolution) are in turn represented as spaces (Lawvere, 2002; Lawvere and Rosebrugh, 2003, pp. 154-155). This productive interplay between spaces and their qualities (theory and broad objective logic; Lawvere, 1994b, 1996, 2004; Lawvere and Rosebrugh, 2003, pp. 235-236, 239-240) moves mathematics towards ever more faithful reflections of space (specifically) and of (more broadly) reality.
References
Cartier, P. (2001) A mad day’s work: From Grothendieck to Connes and Kontsevich; The evolution of concepts of space and symmetry. Bulletin of the American Mathematical Society 38(4): 389-408.
Grothendieck, A. (1983) Pursuing stacks. Bangor: UCNW.
Hopfield, J. J. (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. 79(8): 2554-2558.
Lawvere, F. W. (1975) Continuously variable sets; Algebraic Geometry = Geometric Logic. Studies in Logic and the Foundations of Mathematics 80: 135-156.
Lawvere, F. W. (1992) Categories of space and of quantity. In J. Echeverria, A. Ibarra, and T. Mormann (Eds.), The space of mathematics: Philosophical, epistemological and historical explorations. Berlin: DeGruyter.
Lawvere, F. W. (1994a) Cohesive toposes and Cantor’s lauter Einsen. Philosophia Mathematica 2(1): 5-15.
Lawvere, F. W. (1994b) Tools for the advancement of objective logic: Closed categories and toposes. In J. Macnamara and G. E. Reyes (Eds.) The logical foundations of cognition. New York: Oxford University Press.
Lawvere, F. W. (1996) Adjoints in and among bicategories. Lecture Notes in Pure and Applied Algebra 180: 181-189.
Lawvere, F. W. (2002) Categorical algebra for continuum micro physics. Journal of Pure and Applied Algebra 175: 267-287.
Lawvere, F. W. (2003) Foundations and applications: Axiomatization and education. The Bulletin of Symbolic Logic 9(2): 213-224.
Lawvere, F. W. (2004) Functorial semantics of algebraic theories and some algebraic problems in the context of functorial semantics of algebraic theories. Reprints in Theory and Applications of Categories 5: 1-121.
Lawvere, F. W. (2007) Axiomatic cohesion. Theory and Applications of Categories 19(3): 41-49.
Lawvere, F. W. (2008) Cohesive toposes: Combinatorial and infinitesimal cases.
Lawvere, F. W. (2010) What is a space?
Lawvere, F. W. (2014) Comments on the development of topos theory. Reprints in Theory and Applications of Categories 24: 1-22.
Lawvere, F. W. (2015) Alexander Grothendieck and the modern conception of space.
Lawvere, F. W. and Rosebrugh, R. (2003) Sets for mathematics. Cambridge, UK: Cambridge University Press.
Lawvere, F. W. and Schanuel, S. H. (2009) Conceptual mathematics: A first introduction to categories. 2nd edn. Cambridge, UK: Cambridge University Press.
Lewis, C. (1929) Mind and the world order. New York: Charles Scribner’s Sons.
Picado, J. (2007) An interview with F. William Lawvere. Bulletin of International Center for Mathematics 12: 23-27.
Roskies, A. L. (1999) The binding problem. Neuron 24(1): 7-9.
Roy, S. (1998) Statistical geometry and applications to microphysics and cosmology. The Netherlands: Kluwer Academic Publishers.