Actions of Monoids on Sets
Left actions & Commutative monoids
Let us consider a two-element set
M = {1, i}
with the element ‘1’ as the unit of monoid multiplication
m: M x M ---> M
where
m (1, 1) = 1, m (1, i) = i, m (i, 1) = i, and m (i, i) = 1.
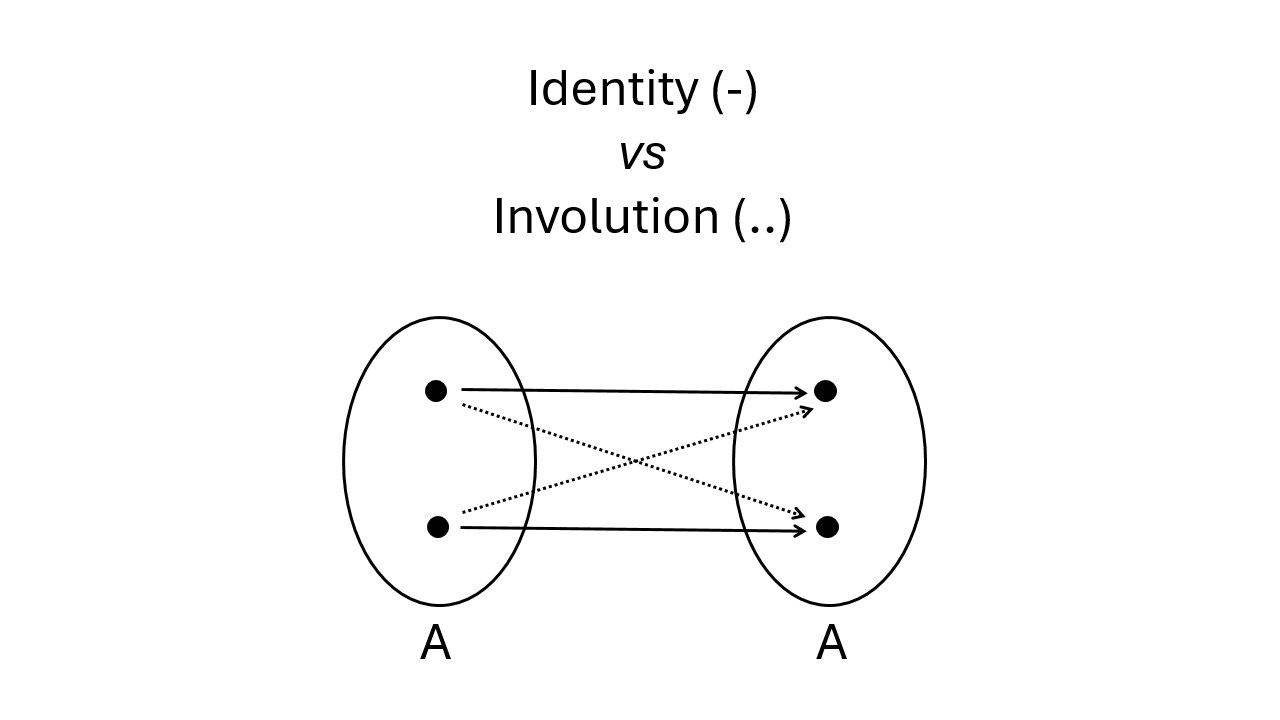
As such, M is a commutative monoid, where i is an involution (think of the two elements of the set M as two endomaps (on a two-element set): identity and involution, with monoid multiplication as composition of endomaps).
Now let us look at the actions of the commutative monoid M on a set A = {a, a’}. Monoid actions are required to be compatible with monoid multiplication, which gives rise to the possibility of left- and right-actions.
It may be of some help to recollect that actions of a set K on a set Q are functions
K x Q ---> Q
which are parameterizations of endomaps on Q by the set K. In the case of sets, given the isomorphism
K x Q ~ Q x K
the parameterization of endomaps on Q has nothing to do whether the parameterizing set K is on the left or right.
However, the actions of sets equipped with monoid structure can result in different parameterizations.
Let’s begin with left-actions of the commutative monoid M on the set A. A left-action of a monoid M on a set A is a function
l: M x A ---> A
compatible with the given monoid multiplication and respectful of the unit of monoid multiplication, all of which boils down to satisfying
l (1, α) = α for all α in A
l (µ, l (µ’, α)) = l (m (µ, µ’), α) for all µ, µ’ in M.
First note that there a total of 16 functions
l: M x A ---> A.
where M = {1, i} and A = {a, a’}.
They are
l1: M x A ---> A ... l16: M x A ---> A
with
l1 (1, a) = a, l1 (i, a) = a, l1 (1, a’) = a, and l1 (i, a’) = a
l2 (1, a) = a, l2 (i, a) = a, l2 (1, a’) = a, and l2 (i, a’) = a’
l3 (1, a) = a, l3 (i, a) = a, l3 (1, a’) = a’, and l3 (i, a’) = a
l4 (1, a) = a, l4 (i, a) = a, l4 (1, a’) = a’, and l4 (i, a’) = a’
l5 (1, a) = a, l5 (i, a) = a’, l5 (1, a’) = a, and l5 (i, a’) = a
l6 (1, a) = a, l6 (i, a) = a’, l6 (1, a’) = a, and l6 (i, a’) = a’
l7 (1, a) = a, l7 (i, a) = a’, l7 (1, a’) = a’, and l7 (i, a’) = a
l8 (1, a) = a, l8 (i, a) = a’, l8 (1, a’) = a’, and l8 (i, a’) = a’
l9 (1, a) = a’, l9 (i, a) = a, l9 (1, a’) = a, and l9 (i, a’) = a
l10 (1, a) = a’, l10 (i, a) = a, l10 (1, a’) = a, and l10 (i, a’) = a’
l11 (1, a) = a’, l11 (i, a) = a, l11 (1, a’) = a’, and l11 (i, a’) = a
l12 (1, a) = a’, l12 (i, a) = a, l12 (1, a’) = a’, and l12 (i, a’) = a’
l13 (1, a) = a’, l13 (i, a) = a’, l13 (1, a’) = a, and l13 (i, a’) = a
l14 (1, a) = a’, l14 (i, a) = a’, l14 (1, a’) = a, and l14 (i, a’) = a’
l15 (1, a) = a’, l15 (i, a) = a’, l15 (1, a’) = a’, and l15 (i, a’) = a
l16 (1, a) = a’, l16 (i, a) = a’, l16 (1, a’) = a’, and l16 (i, a’) = a’
First, let’s see which li (for i = 1, 2 ... 16) are monoid unit-respecting parameterizations:
l (1, α) = α for all α in A
l1 is not a monoid unit-respecting parameterization since l1 (1, a’) = a. So is the case with: l2 (1, a’) = a, l5 (1, a’) = a, l6 (1, a’) = a, l9 (1, a) = a’, l10 (1, a) = a’, l11 (1, a) = a’, l12 (1, a) = a’, l13 (1, a) = a’, l14 (1, a) = a’, l15 (1, a) = a’, and l16 (1, a) = a’.
Thus, we have to check which one of the remaining
l3 (1, a) = a, l3 (i, a) = a, l3 (1, a’) = a’, and l3 (i, a’) = a
l4 (1, a) = a, l4 (i, a) = a, l4 (1, a’) = a’, and l4 (i, a’) = a’
l7 (1, a) = a, l7 (i, a) = a’, l7 (1, a’) = a’, and l7 (i, a’) = a
l8 (1, a) = a, l8 (i, a) = a’, l8 (1, a’) = a’, and l8 (i, a’) = a’
are compatible with monoid multiplication m on the left i.e., satisfy
l (µ, l (µ’, α)) = l (m (µ, µ’), α)
at each one of the 8 elements of the common domain set
M x M x A = {(1, 1, a), (1, 1, a’), (1, i, a), (1, i, a’), (i, 1, a), (i, 1, a’), (i, i, a), (i, i, a’)}
Beginning with
l3 (1, a) = a, l3 (i, a) = a, l3 (1, a’) = a’, and l3 (i, a’) = a
and evaluating at element 1: (1, 1, a)
LHS: l3 (µ, l3 (µ’, α)) at (1, 1, a) = l3 (1, l3 (1, a)) = l3 (1, a) = a
RHS: l3 (m (µ, µ’), α) at (1, 1, a) = l3 (m (1, 1), a) = l3 (1, a) = a
RHS = LHS at (1, 1, a).
@ element 2: (1, 1, a’)
LHS: l3 (µ, l3 (µ’, α)) at (1, 1, a’) = l3 (1, l3 (1, a’)) = l3 (1, a’) = a’
RHS: l3 (m (µ, µ’), α) at (1, 1, a’) = l3 (m (1, 1), a’) = l3 (1, a’) = a’
RHS = LHS at (1, 1, a’).
@ element 3: (1, i, a)
LHS: l3 (µ, l3 (µ’, α)) at (1, i, a) = l3 (1, l3 (i, a)) = l3 (1, a) = a
RHS: l3 (m (µ, µ’), α) at (1, i, a) = l3 (m (1, i), a) = l3 (i, a) = a
RHS = LHS at (1, i, a).
@ element 4: (1, i, a’)
LHS: l3 (µ, l3 (µ’, α)) at (1, i, a’) = l3 (1, l3 (i, a’)) = l3 (1, a) = a
RHS: l3 (m (µ, µ’), α) at (1, i, a’) = l3 (m (1, i), a’) = l3 (i, a’) = a
RHS = LHS at (1, i, a’).
@ element 5: (i, 1, a)
LHS: l3 (µ, l3 (µ’, α)) at (i, 1, a) = l3 (i, l3 (1, a)) = l3 (i, a) = a
RHS: l3 (m (µ, µ’), α) at (i, 1, a) = l3 (m (i, 1), a) = l3 (i, a) = a
RHS = LHS at (i, 1, a).
@ element 6: (i, 1, a’)
LHS: l3 (µ, l3 (µ’, α)) at (i, 1, a’) = l3 (i, l3 (1, a’)) = l3 (i, a’) = a
RHS: l3 (m (µ, µ’), α) at (i, 1, a’) = l3 (m (i, 1), a’) = l3 (i, a’) = a
RHS = LHS at (i, 1, a’).
@ element 7: (i, i, a)
LHS: l3 (µ, l3 (µ’, α)) at (i, i, a) = l3 (i, l3 (i, a)) = l3 (i, a) = a
RHS: l3 (m (µ, µ’), α) at (i, i, a) = l3 (m (i, i), a) = l3 (1, a) = a
RHS = LHS at (i, i, a).
@ element 8: (i, i, a’)
LHS: l3 (µ, l3 (µ’, α)) at (i, i, a’) = l3 (i, l3 (i, a’)) = l3 (i, a) = a
RHS: l3 (m (µ, µ’), α) at (i, i, a’) = l3 (m (i, i), a’) = l3 (1, a’) = a’
RHS ≠ LHS at (i, i, a’). As such,
l3 (1, a) = a, l3 (i, a) = a, l3 (1, a’) = a’, and l3 (i, a’) = a
Is not compatible with monoid multiplication on the left, i.e., the function
l3: M x A ---> A
is not a left-action of the monoid M on the set A.
Next, we evaluate the function
l4 (1, a) = a, l4 (i, a) = a, l4 (1, a’) = a’, and l4 (i, a’) = a’
at element 1: (1, 1, a)
LHS: l4 (µ, l4 (µ’, α)) at (1, 1, a) = l4 (1, l4 (1, a)) = l4 (1, a) = a
RHS: l4 (m (µ, µ’), α) at (1, 1, a) = l4 (m (1, 1), a) = l4 (1, a) = a
RHS = LHS at (1, 1, a).
@ element 2: (1, 1, a’)
LHS: l4 (µ, l4 (µ’, α)) at (1, 1, a’) = l4 (1, l4 (1, a’)) = l4 (1, a’) = a’
RHS: l4 (m (µ, µ’), α) at (1, 1, a’) = l4 (m (1, 1), a’) = l4 (1, a’) = a’
RHS = LHS at (1, 1, a’).
@ element 3: (1, i, a)
LHS: l4 (µ, l4 (µ’, α)) at (1, i, a) = l4 (1, l4 (i, a)) = l4 (1, a) = a
RHS: l4 (m (µ, µ’), α) at (1, i, a) = l4 (m (1, i), a) = l4 (i, a) = a
RHS = LHS at (1, i, a).
@ element 4: (1, i, a’)
LHS: l4 (µ, l4 (µ’, α)) at (1, i, a’) = l4 (1, l4 (i, a’)) = l4 (1, a’) = a’
RHS: l4 (m (µ, µ’), α) at (1, i, a’) = l4 (m (1, i), a’) = l4 (i, a’) = a’
RHS = LHS at (1, i, a’).
@ element 5: (i, 1, a)
LHS: l4 (µ, l4 (µ’, α)) at (i, 1, a) = l4 (i, l4 (1, a)) = l4 (i, a) = a
RHS: l4 (m (µ, µ’), α) at (i, 1, a) = l4 (m (i, 1), a) = l4 (i, a) = a
RHS = LHS at (i, 1, a).
@ element 6: (i, 1, a’)
LHS: l4 (µ, l4 (µ’, α)) at (i, 1, a’) = l4 (i, l4 (1, a’)) = l4 (i, a’) = a’
RHS: l4 (m (µ, µ’), α) at (i, 1, a’) = l4 (m (i, 1), a’) = l4 (i, a’) = a’
RHS = LHS at (i, 1, a’).
@ element 7: (i, i, a)
LHS: l4 (µ, l4 (µ’, α)) at (i, i, a) = l4 (i, l4 (i, a)) = l4 (i, a) = a
RHS: l4 (m (µ, µ’), α) at (i, i, a) = l4 (m (i, i), a) = l4 (1, a’) = a’
RHS ≠ LHS at (i, i, a). As such,
l4 (1, a) = a, l4 (i, a) = a, l4 (1, a’) = a’, and l4 (i, a’) = a’
is not compatible with monoid multiplication on the left, i.e., the function
l4: M x A ---> A
is not a left-action of the monoid M on the set A. Although this inequality at 1 point is enough to conclude that l4 is not a left-action of the monoid M on the set A, let’s evaluate at the remaining point:
@ element 8: (i, i, a’)
LHS: l4 (µ, l4 (µ’, α)) at (i, i, a’) = l4 (i, l4 (i, a’)) = l4 (i, a’) = a’
RHS: l4 (m (µ, µ’), α) at (i, i, a’) = l4 (m (i, i), a’) = l4 (1, a’) = a’
RHS = LHS at (i, i, a’).
Of course, this doesn’t change our conclusion that l4 is not a left-action of the monoid M on the set A.
Next, we evaluate the function
l7 (1, a) = a, l7 (i, a) = a’, l7 (1, a’) = a’, and l7 (i, a’) = a
at element 1: (1, 1, a)
LHS: l7 (µ, l7 (µ’, α)) at (1, 1, a) = l7 (1, l7 (1, a)) = l7 (1, a) = a
RHS: l7 (m (µ, µ’), α) at (1, 1, a) = l7 (m (1, 1), a) = l7 (1, a) = a
RHS = LHS at (1, 1, a).
@ element 2: (1, 1, a’)
LHS: l7 (µ, l7 (µ’, α)) at (1, 1, a’) = l7 (1, l7 (1, a’)) = l7 (1, a’) = a’
RHS: l7 (m (µ, µ’), α) at (1, 1, a’) = l7 (m (1, 1), a’) = l7 (1, a’) = a’
RHS = LHS at (1, 1, a’).
@ element 3: (1, i, a)
LHS: l7 (µ, l7 (µ’, α)) at (1, i, a) = l7 (1, l7 (i, a)) = l7 (1, a’) = a’
RHS: l7 (m (µ, µ’), α) at (1, i, a) = l7 (m (1, i), a) = l7 (i, a) = a’
RHS = LHS at (1, i, a).
@ element 4: (1, i, a’)
LHS: l7 (µ, l7 (µ’, α)) at (1, i, a’) = l7 (1, l7 (i, a’)) = l7 (1, a) = a
RHS: l7 (m (µ, µ’), α) at (1, i, a’) = l7 (m (1, i), a’) = l7 (i, a’) = a
RHS = LHS at (1, i, a’).
@ element 5: (i, 1, a)
LHS: l7 (µ, l7 (µ’, α)) at (i, 1, a) = l7 (i, l7 (1, a)) = l7 (i, a) = a’
RHS: l7 (m (µ, µ’), α) at (i, 1, a) = l7 (m (i, 1), a) = l7 (i, a) = a’
RHS = LHS at (i, 1, a).
@ element 6: (i, 1, a’)
LHS: l7 (µ, l7 (µ’, α)) at (i, 1, a’) = l7 (i, l7 (1, a’)) = l7 (i, a’) = a
RHS: l7 (m (µ, µ’), α) at (i, 1, a’) = l7 (m (i, 1), a’) = l7 (i, a’) = a
RHS = LHS at (i, 1, a’).
@ element 7: (i, i, a)
LHS: l7 (µ, l7 (µ’, α)) at (i, i, a) = l7 (i, l7 (i, a)) = l7 (i, a’) = a
RHS: l7 (m (µ, µ’), α) at (i, i, a) = l7 (m (i, i), a) = l7 (1, a) = a
RHS = LHS at (i, i, a).
@ element 8: (i, i, a’)
LHS: l7 (µ, l7 (µ’, α)) at (i, i, a’) = l7 (i, l7 (i, a’)) = l7 (i, a) = a’
RHS: l7 (m (µ, µ’), α) at (i, i, a’) = l7 (m (i, i), a’) = l7 (1, a’) = a’
RHS = LHS at (i, i, a’).
Since the function
l7 (1, a) = a, l7 (i, a) = a’, l7 (1, a’) = a’, and l7 (i, a’) = a
satisfies
l7 (µ, l7 (µ’, α)) = l7 (m (µ, µ’), α)
at each one of the 8 elements of the common domain set
M x M x A = {(1, 1, a), (1, 1, a’), (1, i, a), (1, i, a’), (i, 1, a), (i, 1, a’), (i, i, a), (i, i, a’)}
the function
l7: M x A ---> A
is a left-action of the monoid M on the set A.
Next, we evaluate the last of the four functions that are monoid unit-respecting, i.e., the function
l8 (1, a) = a, l8 (i, a) = a’, l8 (1, a’) = a’, and l8 (i, a’) = a’
at element 1: (1, 1, a)
LHS: l8 (µ, l8 (µ’, α)) at (1, 1, a) = l8 (1, l8 (1, a)) = l8 (1, a) = a
RHS: l8 (m (µ, µ’), α) at (1, 1, a) = l8 (m (1, 1), a) = l8 (1, a) = a
RHS = LHS at (1, 1, a).
@ element 2: (1, 1, a’)
LHS: l8 (µ, l8 (µ’, α)) at (1, 1, a’) = l8 (1, l8 (1, a’)) = l8 (1, a’) = a’
RHS: l8 (m (µ, µ’), α) at (1, 1, a’) = l8 (m (1, 1), a’) = l8 (1, a’) = a’
RHS = LHS at (1, 1, a’).
@ element 3: (1, i, a)
LHS: l8 (µ, l8 (µ’, α)) at (1, i, a) = l8 (1, l8 (i, a)) = l8 (1, a’) = a’
RHS: l8 (m (µ, µ’), α) at (1, i, a) = l8 (m (1, i), a) = l8 (i, a) = a’
RHS = LHS at (1, i, a).
@ element 4: (1, i, a’)
LHS: l8 (µ, l8 (µ’, α)) at (1, i, a’) = l8 (1, l8 (i, a’)) = l8 (1, a’) = a’
RHS: l8 (m (µ, µ’), α) at (1, i, a’) = l8 (m (1, i), a’) = l8 (i, a’) = a’
RHS = LHS at (1, i, a’).
@ element 5: (i, 1, a)
LHS: l8 (µ, l8 (µ’, α)) at (i, 1, a) = l8 (i, l8 (1, a)) = l8 (i, a) = a’
RHS: l8 (m (µ, µ’), α) at (i, 1, a) = l8 (m (i, 1), a) = l8 (i, a) = a’
RHS = LHS at (i, 1, a).
@ element 6: (i, 1, a’)
LHS: l8 (µ, l8 (µ’, α)) at (i, 1, a’) = l8 (i, l8 (1, a’)) = l8 (i, a’) = a’
RHS: l8 (m (µ, µ’), α) at (i, 1, a’) = l8 (m (i, 1), a’) = l8 (i, a’) = a’
RHS = LHS at (i, 1, a’).
@ element 7: (i, i, a)
LHS: l8 (µ, l8 (µ’, α)) at (i, i, a) = l8 (i, l8 (i, a)) = l8 (i, a’) = a’
RHS: l8 (m (µ, µ’), α) at (i, i, a) = l8 (m (i, i), a) = l8 (1, a) = a
RHS ≠ LHS at (i, i, a). As such,
l8 (1, a) = a, l8 (i, a) = a’, l8 (1, a’) = a’, and l8 (i, a’) = a’
is not compatible with monoid multiplication on the left, i.e., the function
l8: M x A ---> A
is not a left-action of the monoid M on the set A. Although this inequality at 1 point is enough to conclude that l8 is not a left-action of the monoid M on the set A, let’s evaluate at the remaining point:
@ element 8: (i, i, a’)
LHS: l8 (µ, l8 (µ’, α)) at (i, i, a’) = l8 (i, l8 (i, a’)) = l8 (i, a’) = a’
RHS: l8 (m (µ, µ’), α) at (i, i, a’) = l8 (m (i, i), a’) = l8 (1, a’) = a’
RHS = LHS at (i, i, a’).
Of course, this doesn’t change our conclusion that l8 is not a left-action of the monoid M on the set A.
Summing it all, of the possible 16 functions
l: M x A ---> A
only 1 function
l7: M x A ---> A
with
l7 (1, a) = a, l7 (i, a) = a’, l7 (1, a’) = a’, and l7 (i, a’) = a
satisfies
l7 (µ, l7 (µ’, α)) = l7 (m (µ, µ’), α)
at each one of the 8 elements of the common domain set
M x M x A = {(1, 1, a), (1, 1, a’), (1, i, a), (1, i, a’), (i, 1, a), (i, 1, a’), (i, i, a), (i, i, a’)}
and also satisfies
l7 (1, α) = α
for all α in A = {a, a’}. Thus, the function
l7: M x A ---> A
is the only left-action of the monoid M = {1, i}, where 1 and i are the unit and involution of the monoid multiplication, on the set A = {a, a’}.
When thought of as parameterization (p) of the endomaps on A by the elements (1 and i) of the monoid M, we have
p (1) = 1A and p (i) = iA
(1A and iA are identity and involution, respectively, on the set A), which is the function
l7: M x A ---> A
that is the only one compatible with the given monoid multiplication
m: M x M ---> M
where
m (1, 1) = 1, m (1, i) = i, m (i, 1) = i, and m (i, i) = 1.
Question: What’s the moral of the story?
My answer: We tunneled through Himalayas and caught a mouse 😉
Your answer: